Mark Herkommer
July 6, 2024
The Great Pyramid

The Great Pyramid, The Pyramid of Cheops (Khufu), built between 2589 - 2566 BC, stands today as one of the greatest architectural achievements. Its dimensions and orientation have astounded mathematicians and astronomers for centuries. Many subscribe to the belief that only God or god-like space aliens could constructed it. I hope to persuade you, gentle reader, to the contrary.
In my opinion it is time to take a good hard look at the Egyptians and their sciences and try to draw some rational conclusions. I believe that the Pyramid was constructed by the Egyptians and their army of laborers. This was done without any extraterrestrial assistance or metaphysical manifestations. Clear thinking and hard work, a little good fortune, and an interesting mathematical coincidence, but not much more.
The skill of their masonry is beyond dispute. The pyramid was built in about 23 years with about 2.5 million stones. This means that every year 100,000 large blocks (285 per day), weighting an average of 2 1/2 tons must have been quarried, dressed, brought to the building site, and set in place.
Like so many of the baffling ancient monuments, no nation today on Earth
has the technology required or the capital wealth to attempt to duplicate the
majestic works of these lost civilizations.
From all accounts, the Egyptians were meticulous record keepers. From dynastic history to harvest yield to small transactions, ample evidence exists to demonstrate their ability and inclination to keep records.
One can speculate as to the basis for this cultural characteristic: Nile flooding, pharaonic rule, general commerce, etc. One this is certain; contemporaneous cultures did not keep records to the extent that the Egyptians did.
Every civilization has its share of creative individuals. These individuals borrow from their culture and synthesize new information. From the detailed historical records, we know that over time the ancient Egyptians developed a body of abstract information. Historical investigations into the records and buildings of the Egyptians has established they developed and maintained a body of scientific information. These things the ancient Egyptians knew with certainty (in no particular order):

At some point in their history, probably during the 4th dynasty, the ancient Egyptians came to a stunning realization:
the ratio of a circle's circumference to its diameter is a constant
Once recognizing this fact, I am sure it would not be long before they would try to estimate p, probably as 3 1/7. I also believe that they could easily discover that this is only an approximation; that the "true" value of p is more elusive.
On the other hand, just because they did not have a more exact value for
p did not mean that they could not fully exploit
it. Their love of the circle is evident in much of their worship, art, glyphs,
and architecture. The Egyptians were truly a circumphillic society.
In honor of their great discovery, the circumphillic Egyptians found a way to incorporate p into the architecture of Great Pyramid through a simple yet elegant vehicle:
This of course is same formula expressing the relationship between a circle's diameter and its circumference. What is even more interesting is that they did not even need to calculate p to employ it.
By measuring using a wheel having the diameter of 2 units (cubits), they
could roll out the perimeter exactly as many revolutions as the pyramid
was units tall. Although p was never specifically
calculated, its value became incorporated to a very high degree of accuracy.
By some estimates, five decimal places. WOW!!!
How can I assert that the Great Pyramid is a monument to p? If you look at the other finished true pyramids (not step pyramids) of Egypt, you can see the Great Pyramid is one of three that embodies p. These three pyramids, which I shall call "p pyramids", were apparently constructed around the 4th dynasty (ca. 2575 to 2450 BC).
Other mathematical relationships appear to be represented as well. Any relationship that is not within one minute of arc (1/60º) is marked with "?":
| pyramid | location | dynasty | base (meters) |
height (meters) |
face angle (º) |
mathematical relationship |
|---|---|---|---|---|---|---|
| Snofru | Maidum | 3rd/4th | 147 | 93.5 | 51.8431 | p pyramid (renovated step pyramid) |
| Snofru - "Bent Pyramid" Initially built as an equilateral pyramid, the lower section was girdled and the upper section completed with a lower slope angle. |
Dahshur | 4th | 188 | 105 | initial: 60.0000 lower: 54.4622 upper: 43.3667 |
initial: equilateral lower: (unknown) upper: 20:21:29 pyramid (?) |
| Snofru - "Red Pyramid" | Dahshur | 4th | 220 | 104 | 43.3667 | 20:21:29 pyramid (?) |
| Menkaure' | Giza | 4th | 105 | 65.5 | 51.3403 | (unknown) |
| Khufu (Great Pyramid) | Giza | 4th | 230 | 146 | 51.8431 | p pyramid |
| Khephren | Giza | 4th | 214.5 | 143.5 | 53.1300 | 3:4:5 pyramid |
| Sahure' | Abusir | 5th | 78.5 | 47 | 50.1944 | (unknown) |
| Neuserre' | Abusir | 5th | 81 | 51.5 | 51.8431 | p pyramid |
| Neferirkare' | Abusir | 5th | 105 | 70 | 53.1300 | 3:4:5 pyramid |
| Userkaf | Saqqara | 5th | 73.5 | 49 | 53.1300 | 3:4:5 pyramid |
| Wenis | Saqqara | 5th | 57.5 | 43 | 56.3097 | 20:21:29 pyramid on diagonal (?) |
| Izezi | Saqqara | 5th | 78.5 | 52.5 | 53.1300 | 3:4:5 pyramid |
| Teti | Saqqara | 6th | 78.5 | 52.5 | 53.1300 | 3:4:5 pyramid |
| Pepy I | Saqqara | 6th | 78.5 | 52.5 | 53.1300 | 3:4:5 pyramid |
| Merenre' | Saqqara | 6th | 78.5 | 52.5 | 53.1300 | 3:4:5 pyramid |
| Pepy II | Saqqara | 6th | 78.5 | 52.5 | 53.1300 | 3:4:5 pyramid |
| Senwosret III | Dahshur | 12th | 105 | 78.5 | 56.3097 | (unknown) |
| Amenemhet III | Dahshur | 12th | 105 | 81.5 | 57.2639 | 65:72:97 pyramid (?) |
| Amenemhet I | el-Lisht | 12th | 78.5 | 55 | 54.4622 | (unknown) |
| Senwosret I | el-Lisht | 12th | 105 | 61 | 49.3986 | (unknown) |
| Amenemhet III | Hawara | 12th | 100 | 58 | 48.7500 | Golden Rectangle on diagonal (?) |
| Senwosret II | el-Lahun | 12th | 106 | 48 | 42.5833 | (unknown) |
| Khendjer | Saqqara | 13th | 52.5 | 37 | 55.0000 | (unknown) |
There are a number of queen's pyramids that have the same dimensions and face angle, showing a consistency in aesthetic design and building practices.
It is important to observe that there a general climb in face angle over each of the dynasties, but it is not incremental. Early attempts in the 4th dynasty to increase the face angle to 60º failed on at least two occasions.
Most striking is the repeated face angle of 53.1300º, which is the angle created by a triangle having the ratio 3:4:5. This face angle was typical of pyramids constructed during the 6th dynasty (ca. 2350 - 2180 BC).
Similarly, the incorporation of p into the Great Pyramid (Khufu) is almost certainly a deliberate act. Why would Snofru's pyramid in Maidum, first built as a step pyramid in the 3rd dynasty, be renovated to incorporate p? Further, only one other p pyramid was built after the Great Pyramid, Neuserre's at Abusir.
The fact that there are only three p pyramids may speak to the computational difficulties faced in attempting a construction an irrational number as the base:height ratio for the pyramid. It would be clear to the Egyptians that the 3:4:5 ratio is much easier to scale to the face construction and follows the trend of climbing face angles.
The Snofru pyramid at Dahshur (4th Dynasty) has a face angle of 43.3667, which approximates within ¼º the angle of a 20:21:29 triangle (43.6028º). Other pyramids are within a similar margin of error. Because this is a very early true pyramid, it may be that the Egyptians had not yet mastered the process of architecting certain known mathematical relationships into their pyramids. Alternatively it may be based on some other yet unrecognized mathematical fact.
Two other interesting pyramids from the 4th Dynasty are the "Bent" Pyramid at Dahshur and the Ra'djedef pyramid (The "Lost" Pyramid) at Abu Rawash. The Bent Pyramid was originally constructed with a face angle of 60º. Due to apparent structural instability was girdled with a casing having a 54.46º face angle and finished with the upper section having a 43.37º face angle. The Ra'djedef pyramid, although unfinished (or possibly destroyed), has an apparent face angle of 60º. In medial cross-section these pyramid would have been an equilateral triangle; I call this type an equilateral pyramid.
Both pyramids reflect another mathematically important triangle, the equilateral triangle. The equilateral triangle, with its three equal length sides, is easily constructed, architecturally versatile, and is aesthetically pleasing. Although probably not part of the ancient Egyptian mathematical heritage, can be thought of as two right triangles that have the proportions 1:Ö3:2, usually referred to as a 30:60:90 triangle.
These facts are more than mere coincidences. It is clear that the Egyptians
incorporated their acquired fundamental mathematical knowledge into the design
of their pyramids. Further, the incorporated mathematical relationships have
share an important characteristic with the Egyptian Pharaoh perception, both
are eternal. What better way to recognize the spiritual immortality of a
Pharaoh than with immutable enduring mathematical truth?
What the ancient Egyptians almost certainly did not know is a particular mathematical coincidence involving p and f, the Golden Ratio. It is this coincidence that has in large part fueled speculation about outlandish origins of the Great Pyramid.
Recall first that the Golden Ratio is the solution to the quadratic: f + 1 = f2. The solution is the irrational number: f = (1 + Ö5)/ 2.
It is unlikely that the ancient Egyptians could solve this since they did not have mathematical procedures to solve quadratics. However, the equation itself may have been known to them from its geometric interpretation in the Golden Section. It is worth noting that the Golden Section did not make a possible appearance in pyramid until the Amenemhet III pyramid at Hawara of the 12th dynasty (ca. 2000 - 1800 BC).
The Great Coincidence is this:
Compare the values from either side of the equation:
A difference of merely 0.001506... . (Note that since the latter expression
involves the square root of the Golden Ratio, which itself contains a square
root; the final quantity therefore involves finding a quartic root.)

Why I call this the Great Coincidence is because now it appears as though f is also incorporated into the Great Pyramid as well.
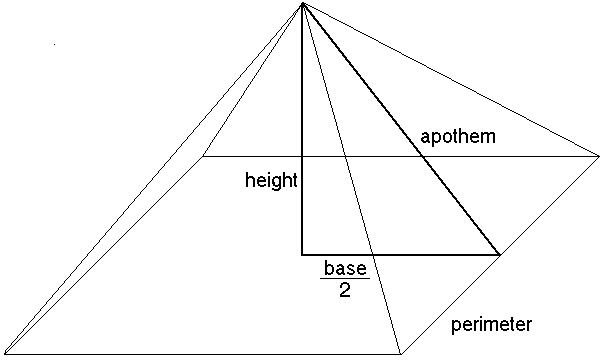
With a little algebraic manipulation we can see that the apothem is in proportion to the base by the Golden Ratio. If we take the base/2 = 1, then we have a triangle with apparent proportions base:height:apothem as 1:Öf:f.
But was this part of the design? No, it was not.
Another interesting relationship occurs because of this coincidence. The area of the face of the pyramid is equal to the height squared.
As before, let base/2 = 1, then using the formula for the area of a triangle:
Of course this is equal to the height squared:
But was this part of the design? Again no, it was not.
All we really have in the ingenious incorporation of one universal constant in a monumental architectural work, and an interesting mathematical coincidence. Furthermore, any p pyramid of any scale must necessarily incorporate these ancillary geometric relationships.
It may come as a disappointment to some that extraterrestrials (or God) did not need tell the Egyptians the value of p or f. The truth is that extraterrestrials (or God) have no more fingerprints on the construction of the Great Pyramid than you or me.
Disappointed? Don't be. Humanity should take pride in the manifest intelligence
of ancient civilizations and purchase hope for future endeavors. I know I do.
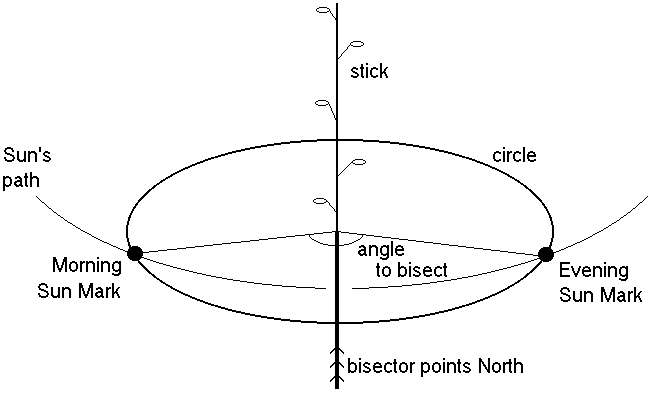
The following procedure will very accurately locate true North. The longer the stick, the greater the accuracy:
© Copyright, 1999-2024. All Rights Reserved.
Mark A. Herkommer